Regressão Logística

Versão em Inglês

Para falar sobre Regressão Logística, usei o mesmo dataset da publicação sobre Regressão Linear Múltipla. Ele contém pontuações de exames que ajudam os alunos a ingressar em faculdades.

A regressão logística usa valores binários para classificar e esse dataset não possui essa informação. Então, para resolver isso eu inseri uma nova coluna Admitted.

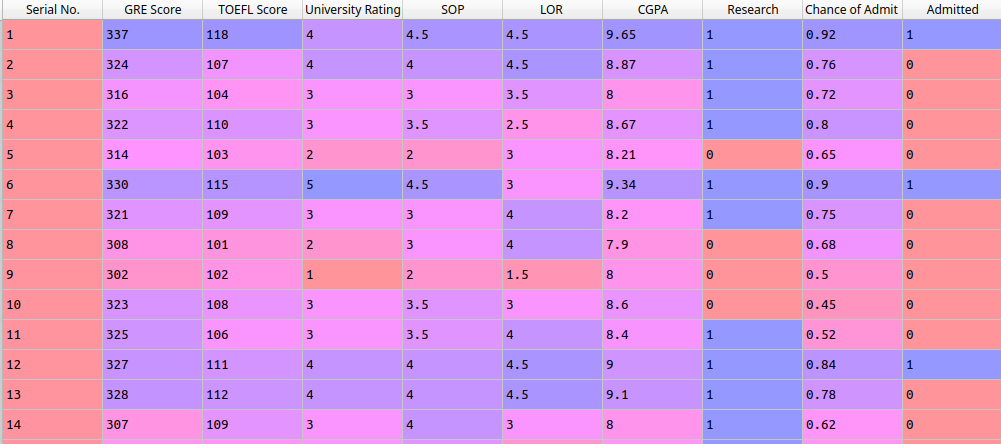
Eu adicionei uma nova coluna com base na coluna Chance of Admit. Se as chances forem maiores que 80%, o valor é 1 senão é 0.

base['Admitted'] = [1 if chance > 0.8 else 0 for chance in base['Chance of Admit ']]

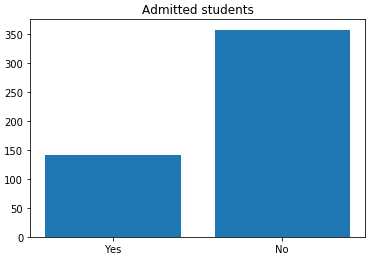
Para obter uma melhor visualização, plotei o gráfico abaixo.

labels = ['Yes', 'No']
x_pos = [0, 1]

admitted = len(base[base['Admitted'] == 1])
not_admitted = len(base[base['Admitted'] == 0])

plt.bar(x_pos, [admitted, not_admitted])
plt.xticks(x_pos, labels)
plt.title('Admitted students')

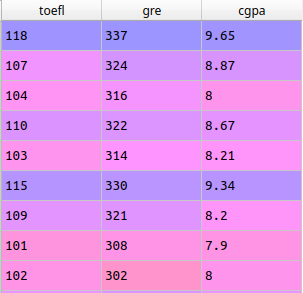
Depois, comecei a preparar os dados. Primeiramente, criei um novo DataFrame apenas com as colunas necessárias.

toefl = base.iloc[:, 2].values
gre   = base.iloc[:, 1].values
cgpa  = base.iloc[:, 6].values

x = pd.DataFrame(np.c_[toefl, gre, cgpa], columns=['toefl','gre', 'cgpa'])

# Coluna Admitted
y = base.iloc[:, -1].values

Separei o dataset em treino e teste.

X_train, X_test, y_train, y_test = train_test_split(x,y, test_size=0.20, random_state=42)

logmodel = LogisticRegression()
logmodel.fit(X_train,y_train)

predictions = logmodel.predict(X_test)

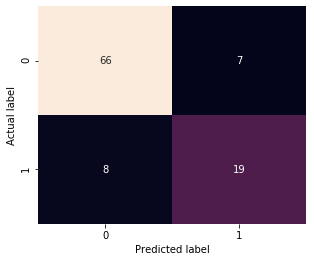
E então eu criei uma matriz de confusão e scores para avaliar os resultado.

cnf_matrix = metrics.confusion_matrix(y_test, predictions)
sns.heatmap(cnf_matrix, annot=True)
plt.ylabel('Actual label')
plt.xlabel('Predicted label')

print("Acurácia: ", metrics.accuracy_score(y_test, predictions))
print("Precisão: ", metrics.precision_score(y_test, predictions))
print("Lembrança: ", metrics.recall_score(y_test, predictions))

# Saída
# Acurácia: 0.85
# Precisão: 0.730769230769
# Lembrança: 0.703703703704

Considerações

Com a matriz de confusão, podemos concluir que:

Verdadeiro positivo: 19 (o modelo previu um resultado positivo e foi positivo).
Verdadeiro negativo: 66 (o modelo previu um resultado negativo e foi negativo).
Falso positivo: 7 (o modelo previu um resultado positivo e foi negativo).
Falso negativo: 8 (o modelo previu um resultado negativo e foi positivo).

e com os scores:

Precisão: 85% foi previsto corretamente.
Precisão: 73% do tempo o modelo está correto sobre suas previsões.
Sensibilidade: 70% do tempo o modelo esperava um resultado positivo.

Os conteúdos que tenho compartilhado são sobre o que estou aprendendo, portanto, se você encontrou algum erro, no código, nos conceitos, nas considerações ortográficas ou até na ortografia, por favor me avise, assim você, me ajudará muito a evitar mais erros.