Regressão Linear Multipla

Versão em Inglês

Neste post, eu quero mostrar como implementei Regressão Linear Múltipla com um dataset sobre graduação que encontrei no Kaggle.

Primeiramente, importei as bibliotecas, o dataset e também verifiquei se existia NaN values (não havia).

import pandas as pd
import matplotlib.pyplot as plt 
import numpy as np
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

base = pd.read_csv('dataset.csv')
base.isna().sum()
base.head()

O dataset possui as seguintes colunas.

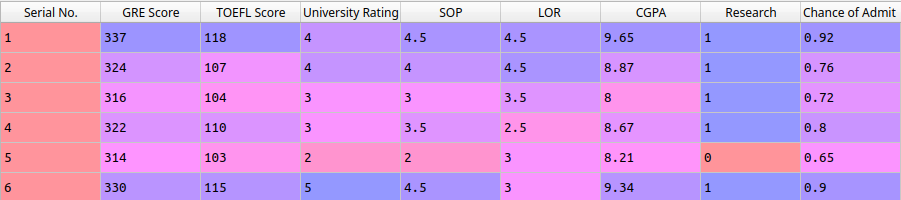
Exibindo os seis primeiros registros com o nome da coluna

Depois disso, como no post de Regressão Linear Simples, eu também usei a biblioteca Seaborn para gerar um gráfico de calor e verificar as correlações entre as variáveis.

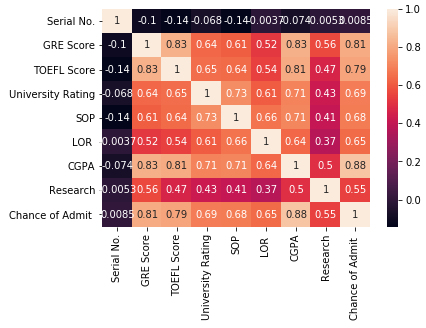
Mapa de calor entre as variáveis do dataset

Eu pude ver que existem fortes correlações entre GRE Score, TOEFL Score e CGPA Score com Chance of Admit, depois plotei gráficos para ter uma visualização melhor.

Armazenei os valores da coluna Change of Admit em uma variável chamada y.

# chance of admit
y = base.iloc[:, -1].values

E então gerei os gráficos.

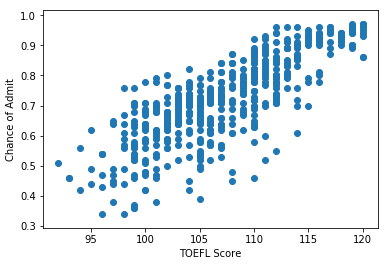
#toefl
toefl = base.iloc[:, 2].values
toefl = toefl.reshape(-1, 1)
plt.scatter(toefl, y)
plt.xlabel('TOEFL Score')
plt.ylabel('Chance of Admit')

Este gráfico mostra a correlação entre TOEFL Score e Chance of Admit

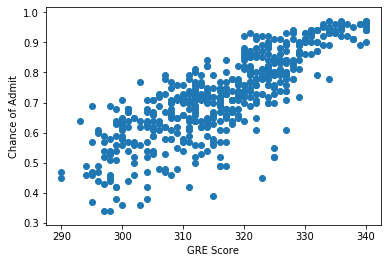
#gre
gre = base.iloc[:, 1].values
gre = gre.reshape(-1, 1)
plt.scatter(gre, y)
plt.xlabel('GRE Score')
plt.ylabel('Chance of Admit')

Este gráfico mostra a correlação entre GRE Score e Chance of Admit

#cgpa
cgpa = base.iloc[:, 6].values
cgpa = cgpa.reshape(-1, 1)
plt.scatter(cgpa, y)
plt.xlabel('CGPA Score')
plt.ylabel('Chance of Admit')

Este gráfico mostra a correlação entre CGPA Score e Chance of Admit

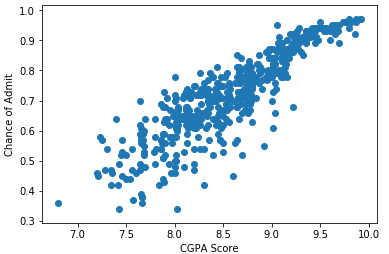
Com as variáveis definidas, construí o modelo para testar. O primeiro passo foi criar um novo DataFrame.

x = pd.DataFrame(np.c_[toefl, gre, cgpa], columns=['toefl','gre', 'cgpa'])
x.head()

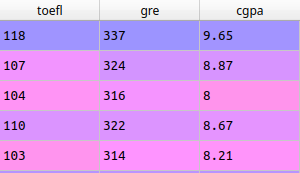
Tabela mostrando as colunas toefl, gre and cgpa

Em seguida, separei o dataset em dois conjuntos de dados.

#20% para testes and 80% para treino
X_train, X_test, Y_train, Y_test = train_test_split(x, y, test_size = 0.2, random_state=42)

Para executar o treino e o teste, fiz o código abaixo usando R2 Score (Coeficiente de Determinação) para ajustar o modelo.

# avaliação de modelo para conjunto de treino
y_train_predict = lin_model.predict(X_train)
r2 = r2_score(Y_train, y_train_predict)

O resultado para o conjunto de treino foi:

print("Desempenho do conjunto de treino")
print("--------------------------------------")
print('O Coeficiente de Determinação é %s' %r2)

# Saída
# Desempenho do conjunto de treino
# --------------------------------------
# O Coeficiente de Determinação é 0.806069903902

Repeti o mesmo processo para o conjunto de testes onde obtive:

# avaliação de modelo para conjunto de testes
y_test_predict = lin_model.predict(X_test)
r2 = r2_score(Y_test, y_test_predict)

print("Desempenho do conjunto de teste")
print("--------------------------------------")
print('O Coeficiente de Determinação é %s' %r2)

# Saída
# Desempenho do conjunto de teste
# --------------------------------------
# O Coeficiente de Determinação é 0.793836133004

Considerações

Os resultados do Coeficiente de Determinação mostraram que é um bom modelo porque os conjuntos de treino e teste ficaram próximos de 1 que é considerado ótimo.

Outro ponto é que para o estudante ter uma chance maior de ser admitido, ele precisa principalmente ter boas pontuações nas váriáveis usadas neste texto.

python regressão linear ciência de dados estatística

Discussion and feedback