Regressão Linear Simples

Versão em Inglês

Hoje eu vou falar sobre os meus estudos com Regressão Linear e mostrar um exemplo simples. Para este conteúdo, eu procurei no Kaggle e encontrei o dataset Beer Consumption - Sao Paulo. Como o nome diz, este possui dados referente ao consumo de cerveja e neste post eu vou mostrar qual dado ajuda a variar o consumo.

Primeiramente, eu importei as bibliotecas e o dataset para visualizar as colunas.

import pandas as pd
import matplotlib.pyplot as plt 
import seaborn as sns
from sklearn.linear_model import LinearRegression

base = pd.read_csv('dataset.csv')
base.head()

Depois disso, eu percebi que havia um monte de linhas em branco.

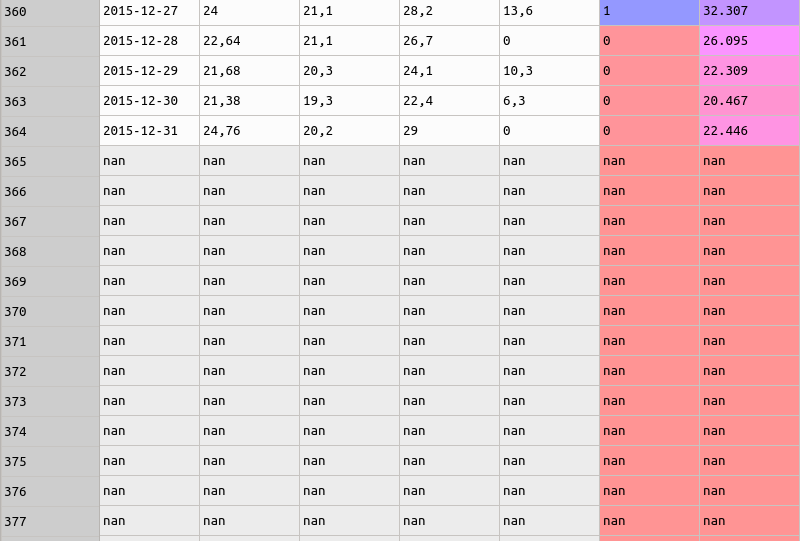
Para ser exato, no dataset havia 576 linhas em branco. Para saber quantas delas eram valores nulos, eu executei o código abaixo.

base.isna().sum()

E obtive a seguinte tabela.

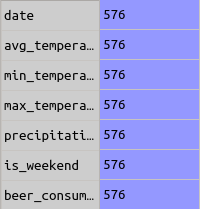
Depois de levantar as informações acima, eu precisei limpar as linhas inúteis. Para fazer isso eu executei:

base = base.dropna()

Então, antes de eu descobrir uma variável que eu usei para correlacionar com beer_consumption eu precisei ver se os dados estavam normalizados.

# pego os valores da última coluna (beer_consumption)
consumption = base.iloc[:, -1].values
plt.hist(consumption)

O código acima exibiu o seguinte gráfico:

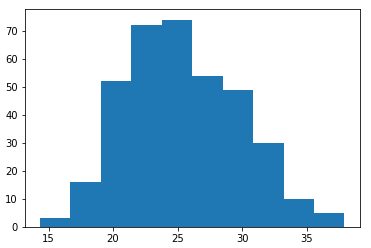
No gráfico, eu vi que os dados estavam normalizados e com esta pré-condição, eu queria saber qual variável correlacionar, entender e prever o consumo de cerveja. Para isso, eu gerei um mapa de calor e eu pude ver qual variável tinha a relação mais forte.

Mas antes de visualizar o gráfico, foi preciso converter as variáveis, porque elas foram importadas como strings.

# substitui vírgula por ponto e converte os valores
base['avg_temperature'] = base['avg_temperature'].str.replace(',', '.')
base['avg_temperature'] = base['avg_temperature'].astype(float)

base['min_temperature'] = base['min_temperature'].str.replace(',', '.')
base['min_temperature'] = base['min_temperature'].astype(float)

base['max_temperature'] = base['max_temperature'].str.replace(',', '.')
base['max_temperature'] = base['max_temperature'].astype(float)

base['min_temperature'] = base['min_temperature'].str.replace(',', '.')
base['min_temperature'] = base['min_temperature'].astype(float)

base['precipitation'] = base['precipitation'].str.replace(',', '.')
base['precipitation'] = base['precipitation'].astype(float)

base['is_weekend'] = base['is_weekend'].astype(bool)

Para gerar o mapa de calor eu usei a biblioteca Seaborn.

sns.heatmap(base.corr(), annot=True)

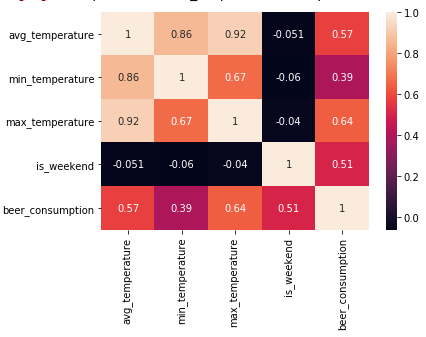
Com a imagem do mapa de calor, eu pude ver melhor a relação entre beer_consumption e max_temperature. A força desta correlação era de 0.64 e tinha uma nível moderado.

Os próximos passos foram entender o comportamento entre ambas variáveis através de um gráfico de dispersão.

# valores do eixo x
x = base['max_temperature'].values
x = x.reshape(-1, 1)
# valores do eixo y
y = base['beer_consumption'].values
plt.scatter(x, y)

Através do gráfico é possível perceber que conforme cresce max_temperature, também aumenta beer_consumption.

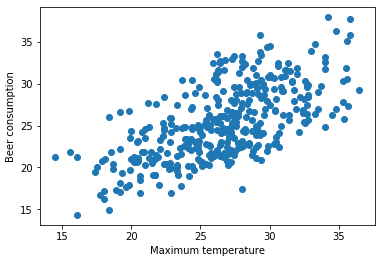
Antes de prever o consumo de cerveja, era preciso treinar os dados.

model = LinearRegression()
model.fit(x, y)

Com os dados treinados, eu mostrei uma linha para os valores que foram previstos.

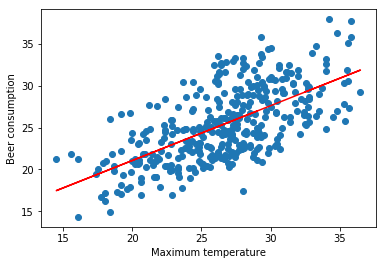
Para finalizar, uma outra experiência é tentar predizer um valor sozinho. Como por exemplo, eu vou tentar prever o consumo de cerveja com uma temperatura máxim de 38º.

model.predict(38)
# Saída: array([ 32.85907157])

Ou seja, com uma temperatura de 38º, o consumo seria de 32 litros.

Eu espero que tenham gostado do post. Qualquer dúvida ou sugestão é só deixar um comentário.